Triangle Center I. Given ΔABC, form its superior
triangle by constructing lines parallel to the sides through the
vertices opposite those sides. This will produce three more
triangles congruent to the original. Construct the circumcircles
of the three new triangles and connect the center of each to the
opposite vertex with three straight lines. Show that those three
lines always meet at a point.
Download: Center1.T
Triangle Center II. Given ΔABC, form its superior
triangle by constructing lines parallel to the sides through the
vertices opposite those sides. This will produce three more
triangles congruent to the original. Construct the nine-point
circles of the three new triangles and connect the center of each
to the opposite vertex with three straight lines. Show that
those three lines always meet at a point. (The nine-point circle
of a triangle is the circle passing through the midpoints of all
three sides.)
Download: Center2.T
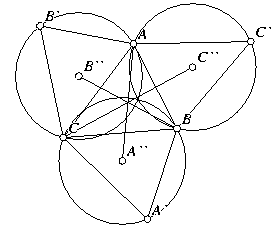Triangle Center III. Given ΔABC, reflect each point
across the opposite side and connect that point to the two
vertices of the opposite side to form three new triangles.
Construct the circumcircles of the three new triangles and
connect the center of each to the opposite vertex with three
straight lines. Show that those three lines always meet at a
point. Also show that the three circumcircles meet at a point.
Download: Center3.T
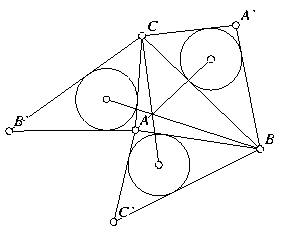Triangle Center IV. Given ΔABC, reflect each point
across the opposite side and connect that point to the two
vertices of the opposite side to form three new triangles.
Construct the incircles of the three new triangles and connect
the center of each to the opposite vertex with three straight
lines. Show that those three lines always meet at a point.
Download: Center4.T
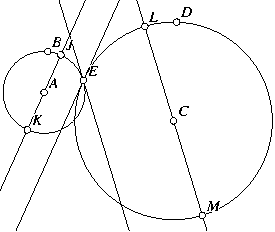Quantum Problem. This problem is from Quantum magazine.
Given two circles that intersect in two points, choose one of the
points of intersection and construct lines tangent to both
circles at that point. Draw diameters of the two circles
parallel to the tangent line of the other circle. Show that the
four points that are the endpoints of the diameters all lie on a
circle.
Download: Quantum.T
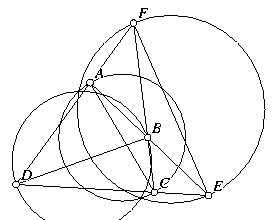Coaxial Circles. If circles are drawn whose diameters are
the diagonals of a complete quadrilateral, those circles are
coaxial. A complete quadrilateral consists of four general lines
and their six intersections. The diagonals are the segments
connecting the pairs of intersections that are not already
connected. Circles are coaxial if there exists a line (the axis)
such that the tangents to the circles from any point on that line
where it makes sense to draw tangents are of equal length.
If the circles intersect, the axis passes through the two points of intersection, so if any two of the three coaxial circles intersect, all three of them do in the same two points.
Download: Gauss.T
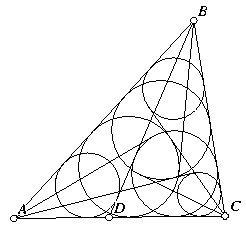Six Circles. This is a problem from the American
Mathematical Monthly. Given any ΔABC, select a point D on
AC, between A and C. Inscribe a circle in ΔDBC. Now draw
the line through A and tangent to that incircle meeting line BC
at a point E. Next, inscribe a circle in ΔAEB. Draw the
line tangent to that incircle from C, and continue in this way,
inscribing circles in the newly-formed triangles and drawing
tangents. Show that after six such circles are inscribed, they
begin to cycle; the seventh circle is the same as the first.
Download: Monthly.T
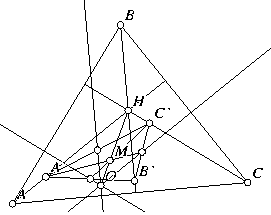Concurrent Perpendiculars. In any ΔABC, let A', B',
and C' be points selected arbitrarily on the altitudes dropped
from points A, B, and C, respectively. Find the midpoints of
ΔA'B'C' and from those three points, drop perpendiculars to
the sides of ΔABC. (Drop the perpendicular from the
midpoint of A'B' to side AB, et cetera.) Show that those three
perpendiculars are concurrent.
Download: Perpmids.T
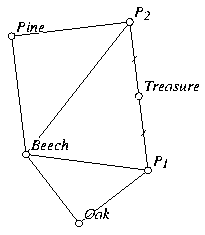Pirate Treasure. Pirates bury treasure with the following
instructions: Start at the beech tree, walk to the oak, turn 90 degrees left and walk the same distance to a point P. Next, start at the beech tree, walk to the pine tree, turn 90 degrees right, and walk the same distance to a point Q. The treasure is at the midpoint of P and Q. But when you get there, the beech tree is missing, but the pine and oak are still standing. How can you find the treasure?
Download: Pirate.T
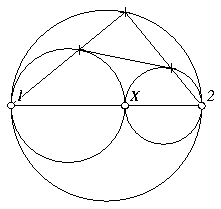Circle Tangent Problem. Two circles are tangent and a
third circle surrounds them having the same diameter as their
common diameter. A common external tangent to the smaller
circles is drawn and it touches the smaller circles in two
points. Lines from the endpoints of the diameter of the larger
circle are drawn through those two points. Show that those lines
meet at a point on the larger circle, and that if a perpendicular
is dropped from this point of intersection to the common
diameter, it will meet the diameter where the two smaller circles
meet.
Download: Zvezda2.T